干货满满丨小白の名词解释小课堂——扩增子相关②

Beta多样性：评估不同微生物群落间整体相似性的数量指数，微生物群落间相似性越低，beta多样性指数越大。

Beta多样性可以分为定性和定量两种：

● 定性的beta多样性指数，包括Jaccard指数、Dice系数等，其只考虑每种OTU在群落中出现/不出现，而不考虑它们的丰度；

●定量的beta多样性指数，包括Bray-Curtis距离、Canberra距离、欧氏距离等，其计算时考虑的是每种OTU在群落中的丰度。

Bray-Curtis距离

：Bray-Curtis距离是以该统计指标的提出者J.Roger Bray和John T. Curtis的名字命名的，主要基于OTUs的计数统计，比较两个群落微生物的组成差异。与unifrac距离，包含的信息完全不一样，相比于jaccard距离，Bray-Curtis则包含了OTUs丰度信息。

UniFrac距离

：在beta多样性的基础上添加了物种进化信息，计算了仅被一个群落占据的进化历史的相对大小，这个量越大，说明两个群落中独立的进化过程越多，也就说明这两个群落的差别越大。举例：若两个群落完全相同，那么它们没有各自独立的进化过程，UniFrac值为0；若两个群落在进化树中完全分开，即它们是完全独立的两个进化过程，那么UniFrac值为1。UniFrac距离分为两种：weighted UniFrac和unweighted UniFrac，unweighted UniFrac在计算时只考虑物种是否在群落中存在，而不考虑其丰度，weighted UniFrac在计算是同时考虑了物种的存在性及其在群落中的相对丰度。

距离矩阵

：样本间的物种或功能的丰度分布差异程度可通过统计学中的距离进行量化分析，使用统计算法Bray-Curtis计算两两样本间距离，获得距离矩阵，可用于后续进一步的beta多样性分析和可视化统计分析。

PCA：即主成分分析（Principal Component Analysis），是一种对数据进行简化分析的技术，这种方法可以有效的找出数据中最“主要”的元素和结构，去除噪音和冗余，将原有的复杂数据降维，揭示隐藏在复杂数据背后的简单结构。PCA运用方差分解，将多组数据的差异反映在二维坐标图上，坐标轴取能够最大反映方差值的两个特征值。如样本组成越相似，反映在PCA图中的距离越近。不同环境间的样本可能表现出分散和聚集的分布情况，PCA结果中对样本差异性解释度最高的两个或三个成分可以用于对假设因素进行验证。

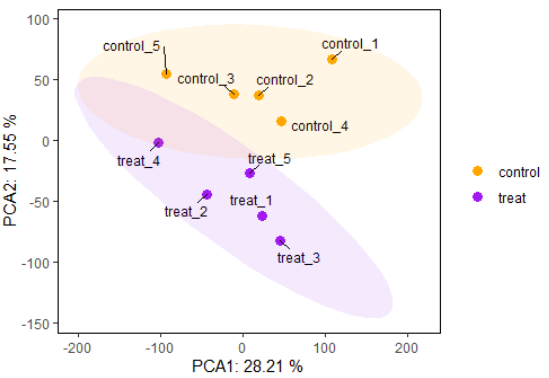
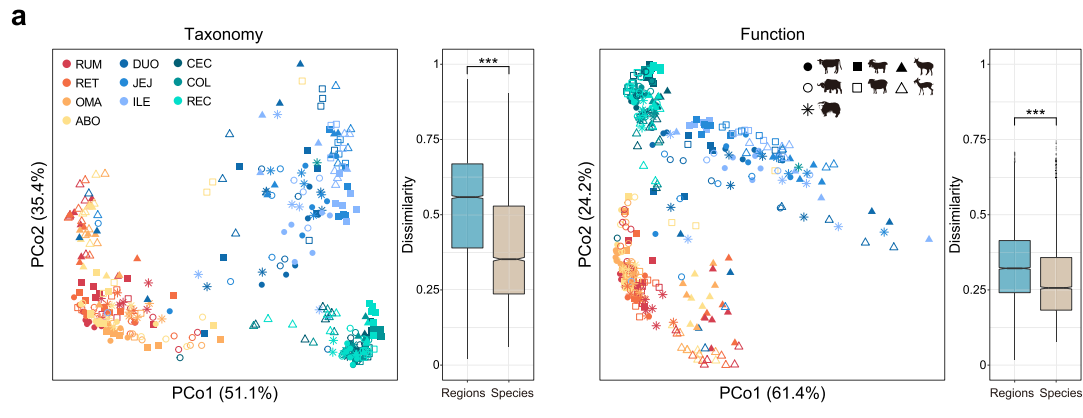
PCoA：主坐标分析（principal co-ordinates analysis），也是一种非约束性的数据降维分析方法，可用来研究样本群落组成的相似性或差异性，与PCA分析类似；主要区别在于，PCA基于欧氏距离，PCoA基于除欧氏距离以外的其它距离，通过降维找出影响样本群落组成差异的潜在主成分。

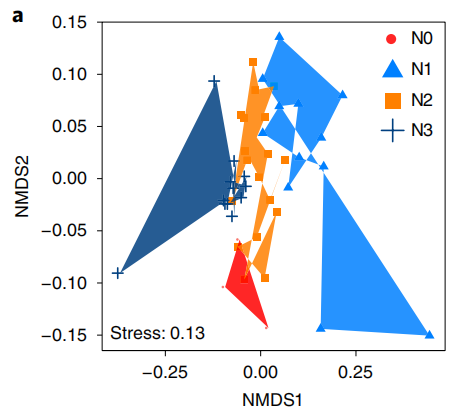
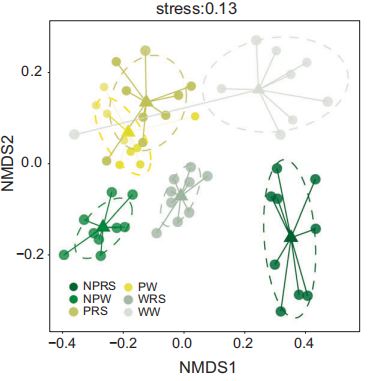
NMDS：即非度量多维尺度分析（NMDS analysis and plot NMDS），是一种将多维空间的研究对象（样本或变量）简化到低维空间进行定位、分析和归类，同时又保留对象间原始关系的数据分析方法，一般用组间样本的秩次（数据排名rank order）上的差异来定义距离。模型的stress值可用于判断该图形是否能准确反映数据排序的真实分布，stress值越接近0则降维效果越好，当stress值小于0.2时，表明NMDS分析具有一定的可靠性。

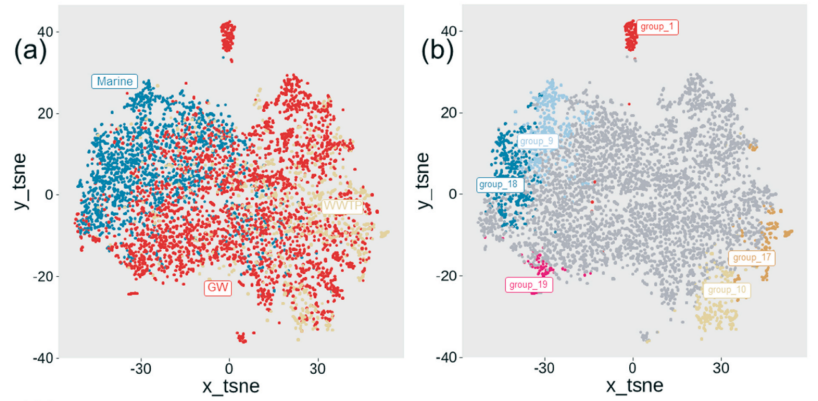
tSNE：t-SNE（t-distributed stochastic neighbor embedding）是用于降维的一种机器学习算法，是由Laurens van der Maaten等在08年提出来。主要是将数据从高维数据转到低维数据，并在低维空间里也保持其在高维空间里所携带的信息（比如高维空间里有的清晰的分布特征，转到低维度时也依然存在）。这一点，跟我们之前学的PCA是有明显差别的，它不仅仅只是简单的映射变换，主要优势在于通过t分布与正态分布的差异，解决了降维后的拥挤问题，使得相似的样本能够聚集在一起，而差异大的样本能够有效地分开，避免了其他降维方法样本分布拥挤、边界不明显的缺点。简而言之就是先选中某一个点，然后计算该点到所有点的距离，然后将所有点映射到对应分布上。可以克服线性降维分类效果差的缺点，对数据完成更好的聚类分析，一般在大样本多分组的时候使用效果比较好。

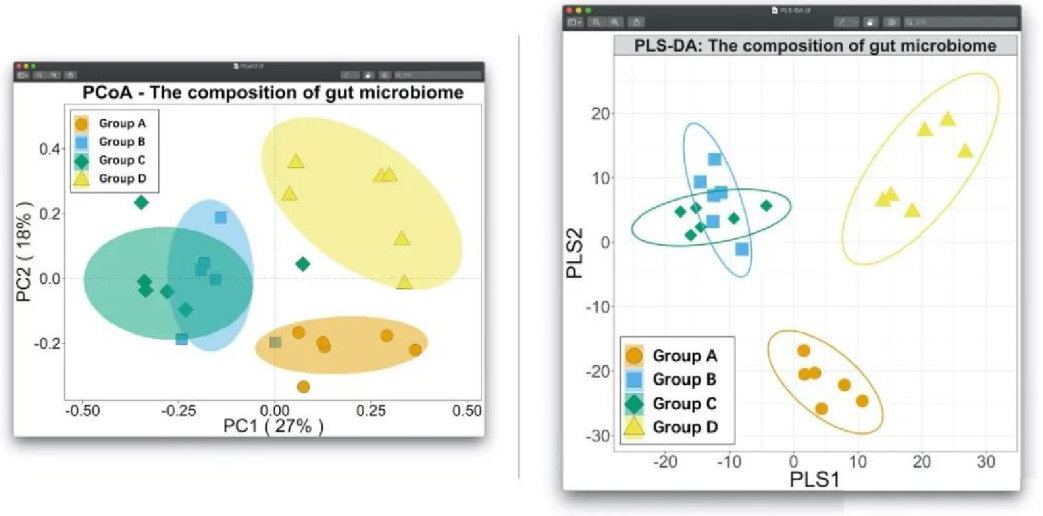
PLS-DA：即偏最小二乘法判别分析（Partial Least Squares Discriminant Analysis），是多变量数据分析技术中的判别分析法，经常用来处理分类和判别问题。通过对主成分适当的旋转，PLS-DA可以有效的对组间观察值进行区分，并且能够找到导致组间区别的影响变量。常见组学文章中一般使用PCA分析降维，但如果样品之间相关性不强的话，这时候PCA降维的效果其实不太好，可以试试用有监督的分析方法PLS-DA，在使用的同时最好也要结合PERMANOVA的组间差异统计学检验结果。

RDA/CCA：RDA或者CCA是基于对应分析发展而来的一种排序方法，将对应分析与多元回归分析相结合，每一步计算均与环境因子进行回归，又称多元直接梯度分析。此分析是主要用来反映菌群与环境因子之间关系。RDA是基于线性模型，CCA是基于单峰模型。分析可以检测环境因子、样本、菌群三者之间的关系或者两两之间的关系。

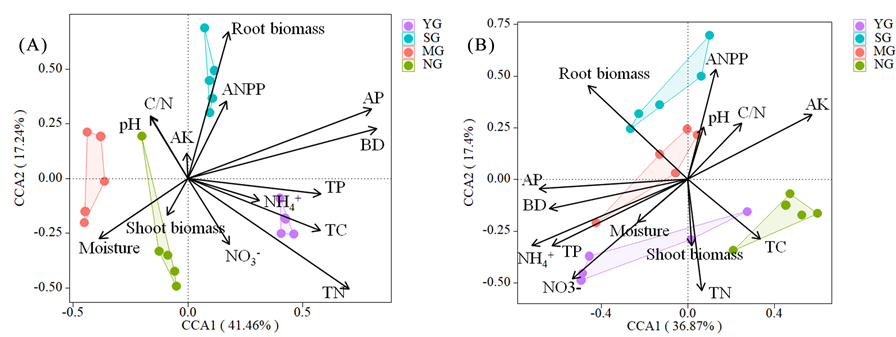
注：图中横纵坐标为两个排序轴，圆点表示样本，不同颜色表示不同分组；箭头表示环境因子，箭头连线的长度代表某个环境因子与群落分布和种类分布间相关程度的大小，箭头越长，说明相关性越大，反之越小；物种与环境因子之间的夹角代表物种与环境因子间的正、负相关关系，锐角为正相关；钝角为负相关；直角为无相关性）；由不同的样本向各环境因子做垂线，投影点越相近说明样本间该环境因子属性值越相似，即环境因子对样本的影响程度相当。

Adonis：又称置换多因素方差分析（permutational MANOVA）或非参数多因素方差分析（nonparametric MANOVA）。它利用半度量（如Bray-Curtis）或度量距离矩阵对总方差进行分解，分析不同分组因素对样品差异的解释度，并使用置换检验对划分的统计学意义进行显著性分析。结果看R2值和Pr值。R2：表示不同分组对样品差异的解释度，即分组方差与总方差的比值，R2越大表示分组对差异的解释度越高；Pr值即P值，表示此次统计分析的可信度， P< 0.05表示统计具有显著性

ANOSIM：相似性分析（ANOSIM）是一种非参数检验，用来检验组间（两组或多组）的差异是否显著大于组内差异，从而判断分组是否有意义。结果看R值和Significance值。R值用于不同组间是否存在差异，Significance值用于说明是否存在显著差异。R值范围为-1到+1，实际中R值一般从0到1。R值接近1表示组间差异越大于组内差异，R值接近0则表示组间和组内没有明显差异；Significance值表示此次统计分析的可信度， Significance值< 0.05表示统计具有显著性。

优势物种（dominant species）：是指在一个生态系统中，当受到外界干扰或者次生演替时，部分物种在竞争中占据大部分资源，排斥其他的物种，最后数量达到绝对优势的物种。

关键物种（keystone species）：是生态系统或生物群落中，对维护生物多样性及其结构、功能及稳定性起关键作用，一旦消失或消弱，生态系统或生物群落就会发生根本性变化的物种。

稀有物种（rare species）：是指群落中个体数目较少的物种，被称为稀有种。在群落的组成中数量不多的稀有种却有较多的种类。